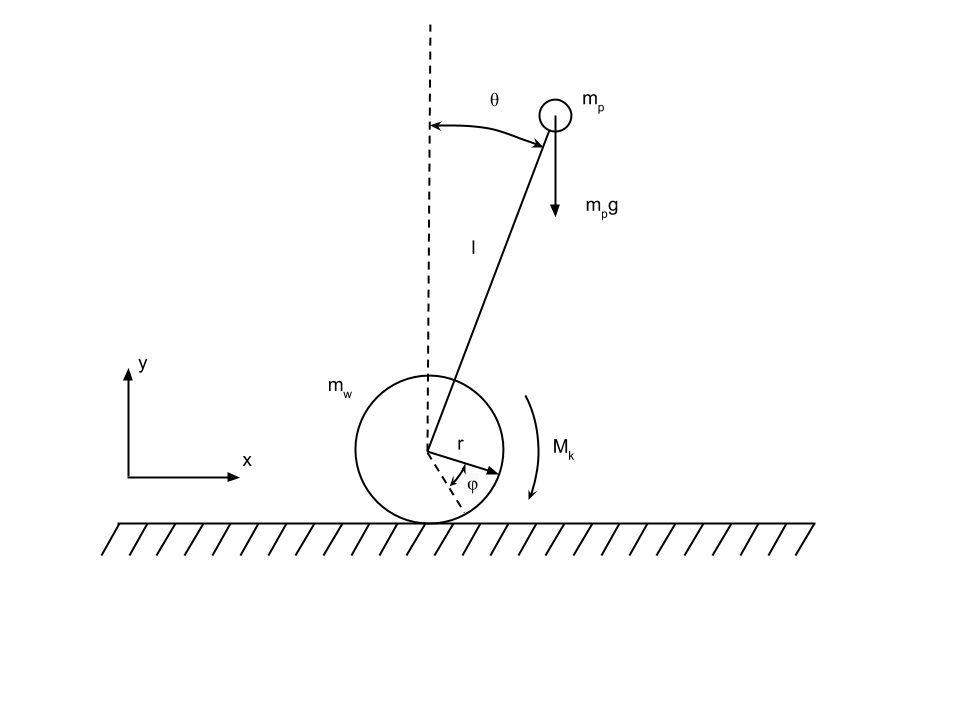
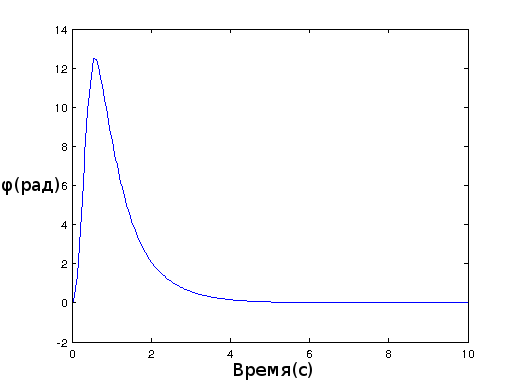
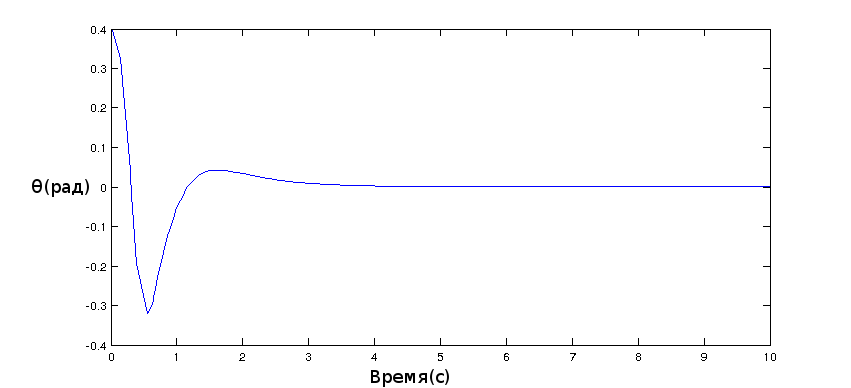
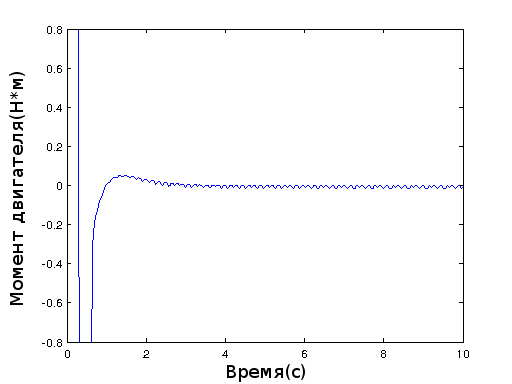
I have build my inverted pendulum robot, finally. The mathematical model and lqr redulator were build to complete the task.
Final result is shown in the video:
float lastCompTime=0;
float filterAngle=1.50;
float dt=0.005;//0.002 //0.005
float comp_filter(float newAngle, float newRate) {
dt=(millis()-lastCompTime)/1000.0;
float filterTerm0;
float filterTerm1;
float filterTerm2;
float timeConstant;
timeConstant=0.5; // default 1.0
filterTerm0 = (newAngle - filterAngle) * timeConstant * timeConstant;
filterTerm2 += filterTerm0 * dt;
filterTerm1 = filterTerm2 + ((newAngle - filterAngle) * 2 * timeConstant) + newRate;
filterAngle = (filterTerm1 * dt) + filterAngle;
lastCompTime=millis();
return filterAngle;
}
On motors quadrature enkoder are established, was to use interruptions to me laziness and I copied a stanadartny code from arduino examples
void doEncoder() {
if (digitalRead(encoder0PinA) == HIGH) {
if (digitalRead(encoder0PinB) == LOW) { // check channel B to see which way
// encoder is turning
encoder0Pos = encoder0Pos - 1; // CCW
}
else {
encoder0Pos = encoder0Pos + 1; // CW
}
}
else // found a high-to-low on channel A
{
if (digitalRead(encoder0PinB) == LOW) { // check channel B to see which way
// encoder is turning
encoder0Pos = encoder0Pos + 1; // CW
}
else {
encoder0Pos = encoder0Pos - 1; // CCW
}
}
}
Further all values of sensors come to the LQR regulator:
float K1=0.1,K2=0.29,K3=6.5,K4=1.12;
long getLQRSpeed(float phi,float dphi,float angle,float dangle){
return constrain((phi*K1+dphi*K2+K3*angle+dangle*K4)*285,-400,400);
}And further value of the regulator arrive on motors. Unfortunately, calculated values of the regulator didn't stabilize the robot and it was necessary to correct them approximately.
Then I added possibility of control from phone. For this purpose I connected bluetooth to pins of serial of port the HC-05 module.
float getPhiAdding(float dif){
if(dif-200){return 0.f;}
float ret = dif*0.08;
return ret;
}
float getFactorAdding(float dif){
if(dif-200){return 0.f;}
float ret = dif/500*20;
Serial.println(ret);
return ret;
}
//==============================================
if (Serial.available()){
BluetoothData=Serial.read();
if(BluetoothData=='w'){
phiDif=200;//constrain(phiDif+10,-200,200);
} else if(BluetoothData=='s'){
phiDif=-200;//constrain(phiDif-10,-200,200);
} else if(BluetoothData=='a'){
factorDif=200;//constrain(factorDif+10,-200,200);
} else if(BluetoothData=='d'){
factorDif=-200;//constrain(factorDif-10,-200,200);
} else if(BluetoothData=='c'){
factorDif=0;//constrain(factorDif-10,-200,200);
phiDif=0;
}
}
encoder0Pos+=getPhiAdding(phiDif);
float factorL=getFactorAdding(factorDif);
md.setSpeeds(spd-factorL,spd+factorL);