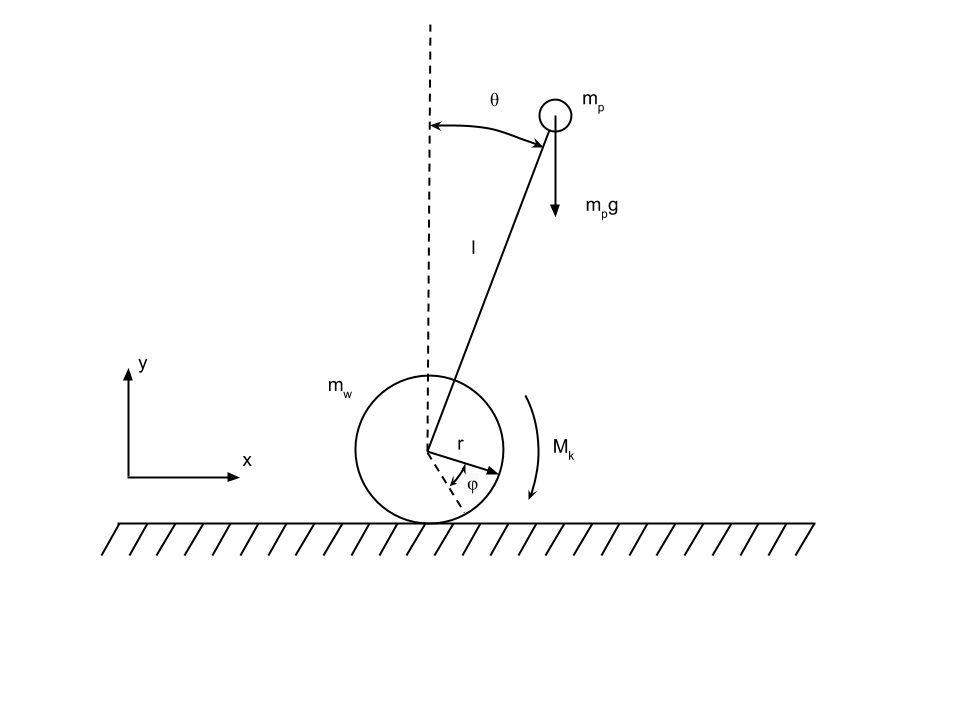
Этапы разработки робота-балансира

2014-04-26

Наконец я завершил постройку робота балансира. Для него была рассчитана математическая модель и линейно-квадратичный регулятор.
Вот, что получилось, оно даже может управляться с телефона:




Сначала я пробовал построить робота на PID регуляторе без всякой математики, но после нескольких дней безуспешных попыток подобрать коэффициенты PID регулятора, я бросил эту затею.

Начнем с расчета математической модели.

Математическая модель


Рассмотрим систему перевёрнутый маятник на колесе, изображённую выше. Будем
считать, что система движется без трения. Маятник представляет собой массу mp,
прикреплённую на невесомом стержне длины l к колесу. Колесо считается кольцом
радиуса r и массой mw. На колесо действует момент двигателя Mk
mp: масса маятника
mw: масса колес
l: длина маятника
r: радиус колеса
θ: угол между маятником и вертикальной прямой
φ:угол поворота колеса относительно его начального положения
Mk: момент двигателя

Для исследования системы воспользуемся уравнениями Эйлера-Лагранжа.
$\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}(q,\dot{q}))-\frac{\partial L}{\partial {q}}(q,\dot{q})=\tau$ (1.1)

Выразим положение центра колеса через угол поворота:
$x=r \phi$ . (1.2)
Заметим, что координаты центра масс маятника находятся по следующим соотношениям:
$x_g =x +l sin (\theta)$ (1.3)
$y_g =l cos(\theta)$ (1.4)
 
Сначала вычислим представление для кинетической энергии системы. Кинетическая
энергия маятника равна
$T_p= \frac{1}{2}[m_p \dot{y}_g^2 (t )+ m_p \dot{x}_g^2(t) ]$ . (1.5)
Кинетическая энергия колеса равна
$T_w= \frac{1}{2}[m_w \dot{x}^2 (t )+ m_w r^2 \dot{\phi}^2(t) ]$ (1.6)
Подставляя (1.2), (1.3),(1.4) в (1.5) и (1.6) получим полную кинетическую энергию
$T= \frac{1}{2}m_p l^2 \dot\theta sin(\theta)^2+ \frac{1}{2}m_p r^2\dot{\phi}^2+ \frac{1}{2}m_p l^2\dot{\theta}^2 cos(\theta)^2+ m_w r^2 \dot{\phi}^2+\frac{1}{2}m_p l^2 \dot{\theta}^2$ (1.7)
Полная потенциальная энергия равна
$\Pi =m_p g l cos (\theta)$
Функция Лагранжа задаётся по формуле $L=T-\Pi$
В итоге
$L=\frac{1}{2}m_p l^2 \dot\theta sin(\theta)^2+ \frac{1}{2}m_p r^2\dot{\phi}^2+ \frac{1}{2}m_p l^2\dot{\theta}^2 cos(\theta)^2+ m_w r^2 \dot{\phi}^2+\frac{1}{2}m_p l^2 \dot{\theta}^2-m_p g l cos(\theta)$

Уравнения движения выведем с помощью уравнений Лагранжа второго рода (1.1).
В качестве обобщённых координат возьмём углы поворота колеса и маятника. Тогда
вектор обобщённых координат представляется в виде
$q=\begin{pmatrix} \phi \\ \theta \end{pmatrix}$
Вектор обобщённых сил выглядит следующим образом:
$\tau=\begin{pmatrix}M_k\\0\end{pmatrix}$
Подставив в уравнения Лагранжа(1.1) производные, выводим уравнения
движения:
$r cos(\theta)l m_p \ddot\theta+r^2(m_p+2m_w)\ddot\phi-rsin(\theta)\theta^2lm_p=M_k$ (1.5)
$\ddot\phi cos(\theta)l m_p r-m_p g l sin(\theta)+2m_pl^2\ddot\theta=0$ (1.6)

Системе можно придать стандартный вид:
$M(q)\ddot q+C(q,\dot q)\dot q+G(q)=\tau$, где 
$q=\begin{pmatrix} \phi \\ \theta \end{pmatrix}$,
$M(q)=\begin{bmatrix}r^2(m_p+2m_w) & r cos(\theta)l m_p\\ r cos(\theta)l m_p & 2 m_p l^2 \end{bmatrix}$,
$C(q,\dot q)=\begin{bmatrix} 0 & -r \dot \theta sin(\theta)l m_p\\  0 & 0 \end{bmatrix}$,
$G(q)=\begin{pmatrix} 0 \\ -m_pg l sin(\theta) \end{pmatrix}$ и
$\tau=\begin{pmatrix}M_k\\0\end{pmatrix}$

Для управления полученной системой построим линейно-квадратичный регулятор.
Для этого проведём линеаризацию полученных уравнений движения (1.5) и (1.6) в
окрестности нулевого положения маятника:
$\frac{d}{dt}\begin{bmatrix} \phi \\ \dot \phi \\ \theta \\ \dot \theta\end{bmatrix}=AX+BM_k=\begin{bmatrix}0 & 1 & 0 & 0\\0 & 0 & \frac{-m_p g}{r(m_p+4m_w)} & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & \frac{g(m_p+2m_w)}{l(m_p+4m_w)} & 0 \end{bmatrix}\begin{bmatrix} \phi \\ \dot \phi \\ \theta \\ \dot \theta\end{bmatrix}+\begin{bmatrix} 0 \\ \frac{2}{r^2(m_p+4m_w)} \\ 0 \\ \frac{1}{l r (m_p+4m_w)}\end{bmatrix}M_k$

Задача оптимального управления подробно разобрана в книге профессора В.Н. Афанасьева «Оптимальные
системы управления. Аналитическое конструирование». В данной статье я не буду останавливаться на ней.

Управление


Управление я вычислял с помощью MatLab, там есть функция lqr, которая вычисляет коэффициэнты. 

Моделирование

Моделирование производил в simulink и вот, что получилось:



Воплощение в железе

Для вычисления угла данные с акселерометра и гироскопа поступают в комплементарный фильтр(RC-фильтр).



float lastCompTime=0;
float filterAngle=1.50;
float dt=0.005;//0.002 //0.005

float comp_filter(float newAngle, float newRate) {

dt=(millis()-lastCompTime)/1000.0;
float filterTerm0;
float filterTerm1;
float filterTerm2;
float timeConstant;

timeConstant=0.5; // default 1.0

filterTerm0 = (newAngle - filterAngle) * timeConstant * timeConstant;
filterTerm2 += filterTerm0 * dt;
filterTerm1 = filterTerm2 + ((newAngle - filterAngle) * 2 * timeConstant) + newRate;
filterAngle = (filterTerm1 * dt) + filterAngle;
lastCompTime=millis();
return filterAngle;
}

На моторах установлены квадратурные энкодеры, использовать прерывания мне было лень и я скопировал станадартный код из примеров arduino


void doEncoder() {
  if (digitalRead(encoder0PinA) == HIGH) {
    if (digitalRead(encoder0PinB) == LOW) {  // check channel B to see which way
                                             // encoder is turning
      encoder0Pos = encoder0Pos - 1;         // CCW
    } 
    else {
      encoder0Pos = encoder0Pos + 1;         // CW
    }
  }
  else                                        // found a high-to-low on channel A
  { 
    if (digitalRead(encoder0PinB) == LOW) {   // check channel B to see which way
                                              // encoder is turning  
      encoder0Pos = encoder0Pos + 1;          // CW
    } 
    else {
      encoder0Pos = encoder0Pos - 1;          // CCW
    }
  }
}

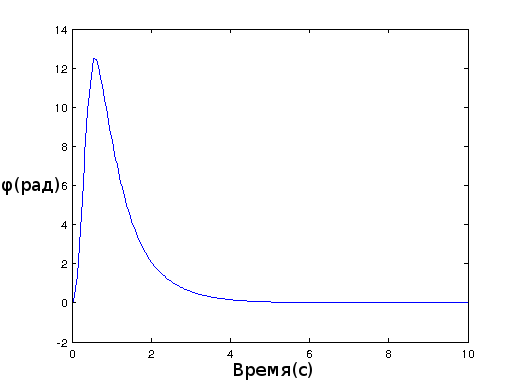
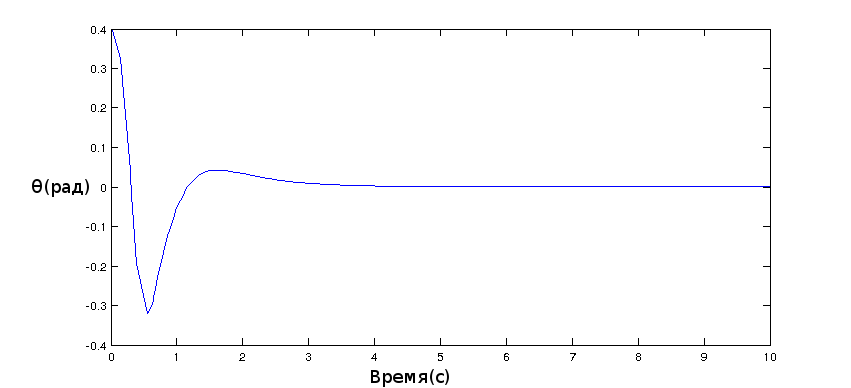
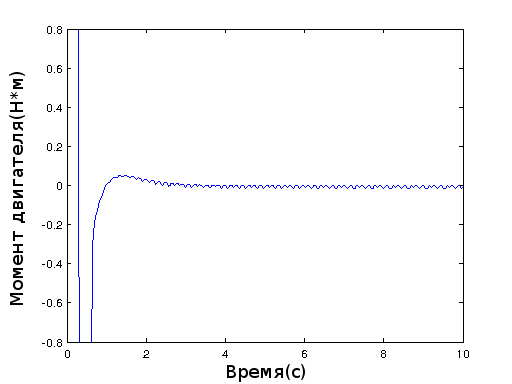
Дальше все значения сенсоров поступают в LQR регулятор:


float K1=0.1,K2=0.29,K3=6.5,K4=1.12;
long getLQRSpeed(float phi,float dphi,float angle,float dangle){
  return constrain((phi*K1+dphi*K2+K3*angle+dangle*K4)*285,-400,400);
}

А дальше значение регулятора поступают на моторы. К сожалению, расчетные значения регулятора не стабилизировали робота и пришлось их подправить на глаз. 
Затем я добавил возможность управления с телефона. Для этого к пинам serial порта подсоединил bluetooth модуль HC-05. 


float getPhiAdding(float dif){

  if(dif-200){return 0.f;}
  float ret = dif*0.08;

  return ret;
}

float getFactorAdding(float dif){
  if(dif-200){return 0.f;}
  float ret = dif/500*20;
  Serial.println(ret);
  return ret;
}
//==============================================
 if (Serial.available()){
    BluetoothData=Serial.read();
     if(BluetoothData=='w'){   
      phiDif=200;//constrain(phiDif+10,-200,200);
     } else if(BluetoothData=='s'){ 
      phiDif=-200;//constrain(phiDif-10,-200,200);      
     } else if(BluetoothData=='a'){   
      factorDif=200;//constrain(factorDif+10,-200,200);
     } else if(BluetoothData=='d'){   
      factorDif=-200;//constrain(factorDif-10,-200,200);      
     } else if(BluetoothData=='c'){   
      factorDif=0;//constrain(factorDif-10,-200,200);      
      phiDif=0;
     }
    }

encoder0Pos+=getPhiAdding(phiDif);
float factorL=getFactorAdding(factorDif);
md.setSpeeds(spd-factorL,spd+factorL);




© Alexander Semion